Силы инерции оказывают не только негативное воздействие. Например, противодействуя на поршне силам действия газов в цилиндре, они разгружают кривошипно-шатунный механизм.
Различают силы инерции при вращательном и возвратно-поступательном движении. Первые также называют центробежными силами. Они возникают при однообразном круговом движении масс. Для расчета центробежных сил инерции используют следующую формулу:
mr — вращающаяся масса;
r — расстояние от центра тяжести массы до ее центра вращения;
ω — угловая скорость.
Силы инерции при возвратно-поступательном движении вызываются, в частности, неравномерным движением поршня. Они рассчитываются по формуле:
mos — масса, движущаяся возвратнопоступательным образом;
α — ускорение поршня.
Если рассчитывать ускорение поршня согласно уравнению 2.6, для сил инерции при возвратно-поступательном движении формула будет следующая:
В роторно-поршневом двигателе вследствие взаимодействия массы ротора mK и массы эксцентрика mE возникают только центробежные силы инерции. Обе массы вращаются с эксцентриситетом е вокруг центра картера с частотой вращения эксцентрикового вала. Формула для центробежных сил инерции роторно-поршневого двигателя является следующей:
В поршневом двигателе расчет центробежных сил инерции немного затруднителен. В этом случае к вращающимся массам относятся шатунная шейка, два плеча кривошипа (противовесы коленчатого вала) и вращающаяся часть (массовая доля) шатуна (рис. 2.11).
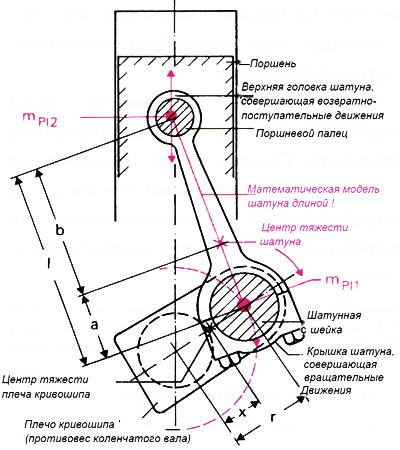
Рис. 2.11. Математическая модель шатуна
Силы инерции вращающейся части шатуна определяются примерным образом с помощью математической модели шатуна длиной l, поскольку движение центра тяжести шатуна нельзя рассчитать с помощью обычных формул. Дело в том, что верхний конец шатуна, соединенный через поршневой палец с поршнем, выполняет лишь возвратно-поступательные движения, а нижний конец шатуна вращается вместе с шатунной шейкой вокруг центра коленчатого вала. Для математической модели шатуна принято считать, что ее масса mPl состоит из двух частей (массовых долей), одна из которых — mPl2 — движется возвратно-поступательным образом вместе с поршнем, а другая — mPl1 — вращается вместе с шатунной шейкой. Так как механические характеристики данной математической модели являются приближенными, как и механические характеристики фактического шатуна, необходимо выполнить следующие расчеты:
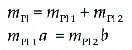
Из данных двух уравнений можно получить соотношения:
Масса mPl1 является вращающейся массовой долей шатуна.
Центры тяжести вращающихся масс кривошипно-шатунного механизма в поршневом двигателе находятся на различном расстоянии от центра вращения, поэтому для расчетов все массы снижаются на величину радиуса поршня г. При этом действительно присутствующие массы преобразовываются в условные массы, которые должны быть настолько велики, чтобы они самостоятельно вызывали возникновение центробежных сил. Формула для снижения массы следующая:
mE — условная масса;
mx — действительная масса;
x — расстояние действительной массы от центра вращения;
r — расстояние условной массы от центра вращения.
Шатунная шейка и вращающаяся массовая доля шатуна находятся на расстоянии r от центра вращения и поэтому не должны уменьшаться. Масса плеча кривошипа, наоборот, должна уменьшаться.
Формула для центробежной силы инерции роторно-поршневого двигателя:
mZ — масса шатунной шейки;
mPl1 — вращающаяся массовая доля шатуна;
2mW — удвоенная масса плеча кривошипа (поскольку шатунная шейка держится на двух противовесах);
r — радиус кривошипа.
В простейшем поршневом двигателе общая масса деталей, двигающихся возвратно-поступательным образом, включает в себя массы поршня, поршневых колец, поршневого пальца и массовую долю шатуна mPl2. Сила инерции при возвратно-поступательном движении рассчитывается по формуле:
mK — общая масса поршня;
mPl2 — массовая доля шатуна, двигающаяся возвратно-поступательным образом.
