Силы инерции, которые возникают в отдельных цилиндрах, рассчитываются по формуле, приведенной в разделе 2.8.1. Данные отдельные силы объединяют только для определения равнодействующей. При хорошей балансировке сил равнодействующая будет равна нулю или же ее значение будет небольшим.
Так как отдельные силы не прикладываются к центру масс двигателя, возникают дополнительные моменты инерции, которые также должны суммироваться для равнодействующей.
Величины всех таких равнодействующих сильно зависят от формы коленчатого вала. Соответственно, вал должен быть сконфигурирован таким образом, чтобы отдельные силы сами себя уравновешивали. При решении данной задачи должны определяться равнодействующие для различных конфигураций коленчатого вала. Быстрее всего это можно выполнить, используя графический метод.
Равнодействующие вращательных сил инерции
Вначале необходимо схематически изобразить коленчатый вал в продольном и поперечном разрезе (рис. 2.24). Поперечное сечение, которое должно находиться слева от продольного разреза, называется из-за своего вида схемой расположения кривошипов. Нумерация кривошипов производится по продольному разрезу коленчатого вала, а затем переносится на схему расположения кривошипов. Вращательные силы инерции каждого цилиндра рассчитываются по уравнению 2.11.
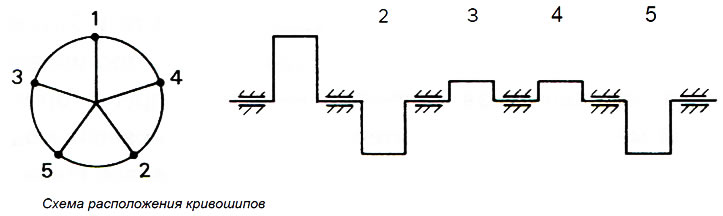
Рис. 2.24. Схема расположения кривошипов и схематический продольный разрез коленчатого вала пятицилиндрового двигателя
Затем, после выбора соответствующего масштаба, силы инерции графически изображаются на одной схеме в виде векторов. Методом векторного сложения получается схема действия сил инерции (рис. 2.25), на которой отдельные силы добавляются к равнодействующей FrR и переносятся на схему расположения сил инерции (рис. 2.25), которая имеет тот же вид, что и схема расположения кривошипов.
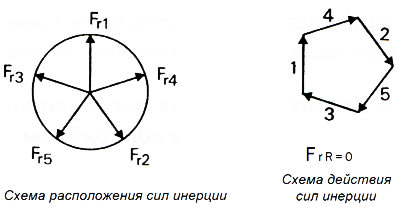
Рис. 2.25. Графическое определение равнодействующей сил инерции F для коленчатого вала пятицилиндрового двигателя
Равнодействующая FrR имеет постоянной величину. Соответственно, вектор равнодействующей на схеме будет иметь постоянную длину, и для разных положений коленчатого вала нет необходимости заново рассчитывать равнодействующую, достаточно лишь повернуть вектор на угол, соответствующий заданному углу поворота коленчатого вала.
В однорядных двигателях с равномерным порядком зажигания и более, чем двумя цилиндрами, равнодействующая равняется нулю.
Равнодействующие сил инерции 1-го порядка
Сила инерции 1-го порядка рассчитывается по уравнению 2.27. Ее максимальное значение равно:
Текущее значение можно получить графически, когда максимальное значение сил инерции указывается в виде вектора в направлении плеча кривошипа и на схеме проецируется на оси цилиндра (рис. 2.26). При определении равнодействующей необходимо, согласно указанному способу, определить все текущие значения сил инерции 1 -го порядка, а затем векторно их суммировать. Данный способ затруднителен.
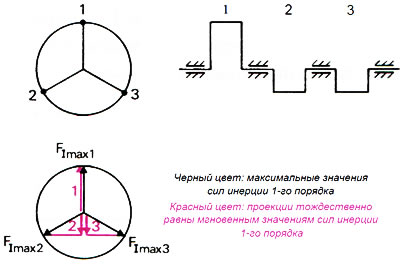
Рис. 2.26. Графическое определение текущих значений сил инерции 1-го порядка
Такую равнодействующую можно получить проще, если сначала перенести все максимальные значения в виде векторов в направлении плеча кривошипа и суммировать эти силы на схеме действия сил инерции (рис. 2.27). Полученные таким способом равнодействующие, то есть равнодействующие максимальных значений FIImaxR, проецируются на ось цилиндра. Данная проекция является искомой равнодействующей сил инерции 1-го порядка FII R.
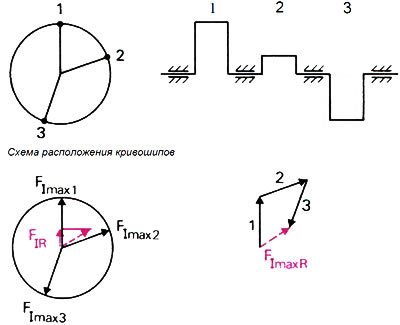
Рис. 2.27. Графическое определение равнодействующей сил инерции 1-го порядка FI R для коленчатого вала трехцилиндрового двигателя с неравномерным порядком зажигания
FII R для трехцилиндрового коленчатого вала с неравномерным порядком зажигания.
Так как схемы действия вращательных сил инерции и сил инерции 1-го порядка похожи даже по длине векторов, очевидным является то, что при исчезновении равнодействующей вращательных сил инерции, равнодействующая сил инерции 1-го порядка будет равна нулю.
Если повернуть коленчатый вал, вместе с его поворотом изменится направление равнодействующей максимального значения. Для нового положения коленчатого вала необходимо спроецировать эту же равнодействующую максимального значения на ось цилиндра, и таким образом получить искомую равнодействующую сил инерции 1-го порядка.
Равнодействующие сил инерции 2-го порядка
Сила инерции 2-го порядка рассчитывается по уравнению 2.28. Возникновение сил инерции 2-го порядка происходит в соответствии с удвоенной частотой вращения коленчатого вала. При этом на оси цилиндра эта сила действует как сила инерции 1-го порядка.
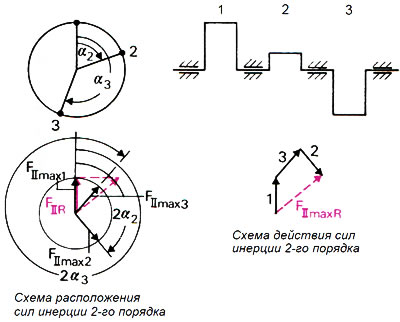
Рис. 2.28. Графическое определение равнодействующей сил инерции 2-го порядка FII R для коленчатого вала трехцилиндрового двигателя с неравномерным порядком зажигания
Для определения равнодействующей так же, как и в случае определения сил инерции 1-го порядка, максимальные значения каждой отдельной силы переносятся на схему расположения сил инерции (рис. 2.28). Данные силы не совпадают из-за «cos 2 α» с плечом кривошипа на схеме расположения кривошипов. На схеме расположения сил инерции 2-го порядка все силы должны наноситься сообразно удвоенной величине угла α. На схеме действия сил инерции они складываются, образовывая равнодействующую максимального значения FIImaxR все вместе переносятся на схему расположения сил. Проекция равнодействующей максимального значения FIImaxR на вертикальную ось цилиндра является искомой равнодействующей сил инерции 2-го порядка FII R.
Если повернуть коленчатый вал на угол α, равнодействующая максимального значения повернется на схеме расположения сил на угол 2α. Новая искомая равнодействующая является ее проекцией на ось цилиндра.
Результирующий момент инерции
Так как силы инерции имеют плечо относительно центра тяжести двигателя, возникают моменты инерции, которые рассчитываются путем умножения силы на расстояние (величину плеча) от центра тяжести. Для их точного определения сначала надо определить положение центра тяжести двигателя. Чаще пренебрегают данной трудоемкой работой и принимают в качестве центра тяжести двигателя точку в центре коленчатого вала. Исходной, или базовой, точкой для расчета моментов инерции считается центр коленчатого вала, определенный на продольном разрезе вала.
Точно так же, как и силу, момент инерции можно представить в виде вектора.
Величина момента инерции в графическом изображении выражается вектором рассчитанной длины. Вектор располагается перпендикулярно плоскости действия момента и своей вершиной указывает направление, в котором перемещался бы болт с правой резьбой, если бы его вращали по направлению действия момента.
Так как вектор момента может сдвигаться вдоль плоскости действия момента, все векторы изображаются перпендикулярно плоскости поперечного сечения, идущей через середину коленчатого вала и, одновременно, через оси цилиндров (рис. 2.29). Получаемую таким образом схему расположения моментов можно создать также с помощью схемы расположения кривошипов. При этом все векторы моментов должны быть указаны на чертеже как соответствующие плечи кривошипов, повернутые на 90° по часовой стрелке.
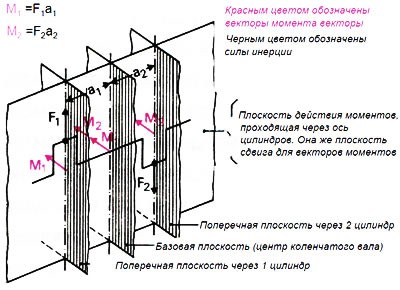
Рис. 2.29. Векторы моментов
Векторы, которые отображают моменты инерции кривошипов, расположенных слева от базовой точки, направлены наружу от центра схемы расположения моментов инерции (Мr1 и Mr2 рис. 2.30).
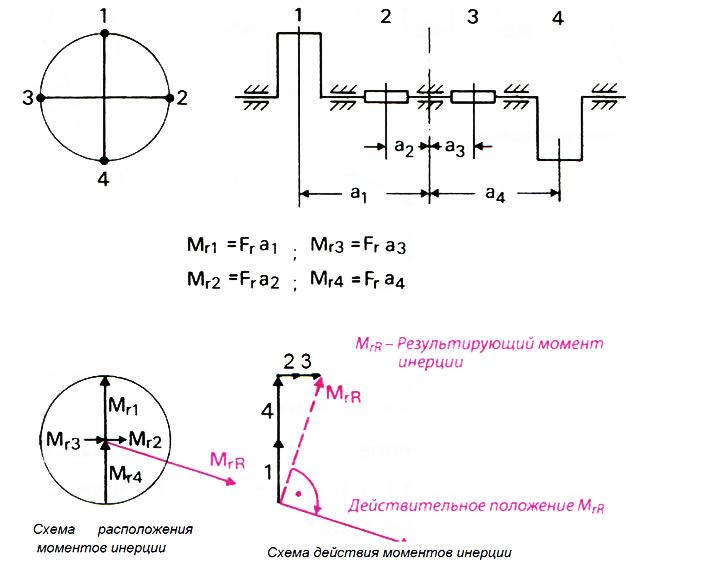
Рис. 2.30. Графическое определение результирующего момента инерции MrR для коленчатого вала четырехцилиндрового двигателя
Векторы, которые отображают моменты инерции кривошипов, расположенных справа от базовой точки, направлены внутрь к центру схемы расположения моментов инерции (Мr3 и Мr4, рис. 2.30).
Получаемый в результате результирующий момент инерции можно определить еще проще, если не указывать отдельные векторы повернутыми на 90° по часовой стрелке, а изображать их просто как плечи кривошипа. После того, как данные векторы будут добавлены к результирующему MrR на схеме действия моментов, путем поворота проекции на 90° по часовой стрелке получаем вектор результирующего момента в действительном положении (рис. 2.30).
Результирующий момент инерции 1-го порядка
Возвратно-поступательные силы инерции действуют только на оси цилиндра. Все векторы моментов расположены перпендикулярно плоскости, проходящей через все оси цилиндров.
При определении результирующих моментов инерции следуют тому же способу, что и при построении равнодействующей сил инерции 1-го порядка на основании максимальных значений. Затем для всех цилиндров рассчитываются максимальные значения моментов. Их необходимо указать на схеме расположения, используя способ указанный в разделе 2.8.2.4 (рис. 2.31). После того, как результирующий момент MImaxR будет построен на схеме действия моментов, его необходимо перенести на схему расположения моментов и спроецировать на ось цилиндра. Повернутая на 90° по часовой стрелке проекция представляет собой фактический результирующий момент инерции 1-го порядка MI R.
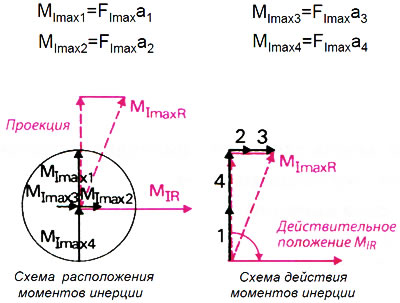
Рис. 2.31. Графическое определение результирующих моментов инерции 1-го порядка MI R для коленчатого вала, изображенного на рис. 2.30
Результирующий момент инерции 2-го порядка
Векторы моментов инерции 2-го порядка расположены перпендикулярно плоскости оси цилиндров, и их величина изменяется в зависимости от удвоенного угла поворота кривошипа. После расчета максимальных значений моментов инерции 2-го порядка необходимо перенести их векторы на схему расположения моментов с размещением под удвоенным углом поворота кривошипа (рис. 2.32). Результирующий момент, полученный на схеме действия моментов, MIImaxR переносится на схему расположения моментов и проецируется на ось цилиндра. Действительный вектор результирующего момента инерции 2-го порядка MII R получаем путем поворота проекции на 90° по часовой стрелке.
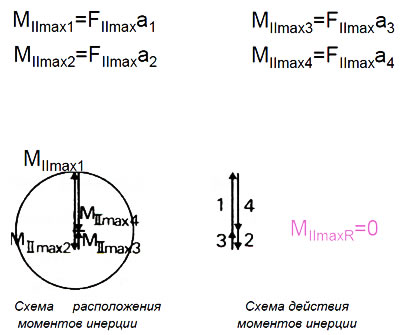
Рис. 2.32. Графическое определение результирующих моментов инерции 2-го порядка MII R для коленчатого вала, изображенного на рис. 2.30
Пример 5
Для изображенного коленчатого вала пятицилиндрового двигателя (рис. 2.33) необходимо определить равнодействущие сил инерции и результирующие моменты инерции. Дано:
- mos = 10 кг
- mr =14 кг
- n =1000 мин-1
- λ = 0,25
- Н =180 мм
- а = 300 мм
- r = 9 см = 0,09 м
Решение
Для начала для одного цилиндра выполняются следующие расчеты:
сила инерции
максимальное значение силы инерции 1-го порядка
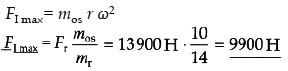
максимальное значение силы инерции 2-го порядка
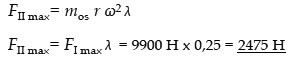
Вышеуказанные значения являются действительными для всех цилиндров из-за их равных размеров.
В качестве масштаба отображения векторов силы выбираются следующие соотношения:
На рис. 2.33.А представлены схема расположения и схема действия сил инерции. Все равнодействующие равны нулю.
Следующий шаг — расчет моментов инерции:
моменты инерции для
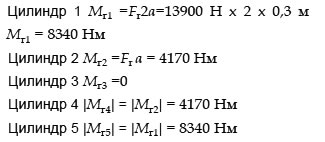
максимальные значения моментов инерции 1-го порядка
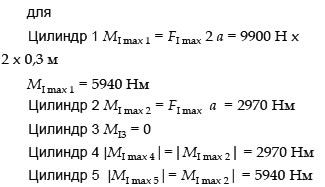
максимальные значения моментов инерции 2-го порядка
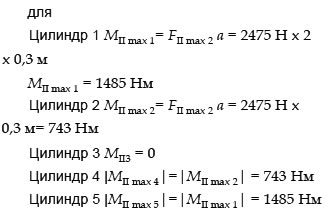
В качестве масштаба отображения векторов моментов выбираются следующие соотношения:
- Для моментов инерции 1 см = 5000 Нм
- Для моментов инерции 1-го порядка 1 см = 2000 Нм
- Для моментов инерции 2-го порядка 1 см = 1000 Нм
На рис. 2.33.В изображены схема расположения и схема действия моментов инерции и получены результирующие моменты.
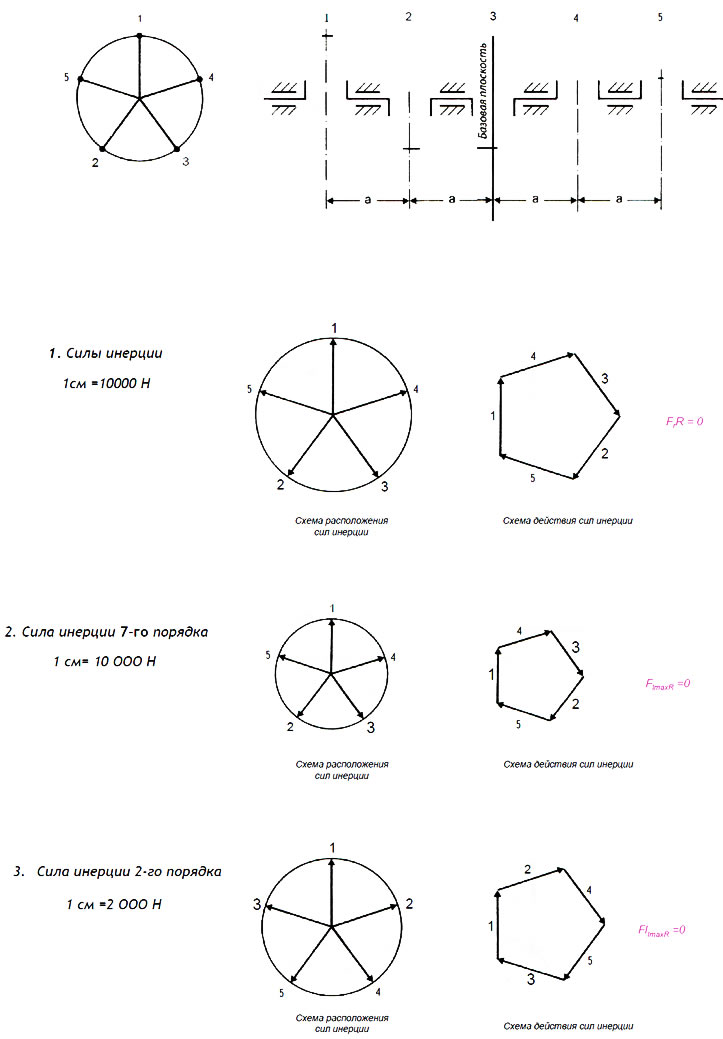
Рис. 2.33.А. Силы инерции коленчатого вала пятицилиндрового двигателя (Пример 5)
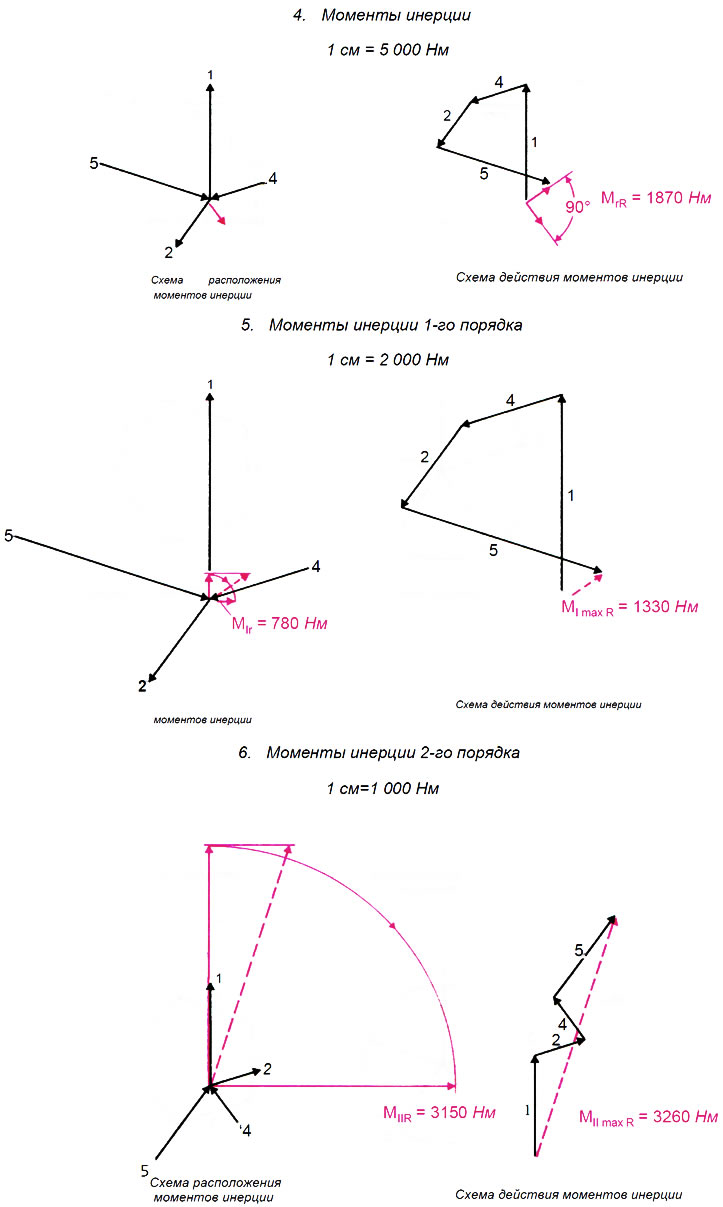
Рис. 2.33.В. Моменты инерции коленчатого вала пятицилиндрового двигателя. (Пример 5)
